Le gradient d'attractivité

Un modèle très simple qui décrit une relation générale entre pouvoir d’attraction du centre, mobilité et densité de la périphérie.

Vers la fin du XIXe siècle, l’avènement puis la généralisation des transports mécanisés ont permis à nos villes de s’étaler dans l’espace et de devenir ce que j’ai appelé ici même des villes du deuxième âge. Le modèle le plus simple de ce type d’agglomérations, c’est le modèle monocentrique : un quartier des affaires central, très dense, autour duquel rayonnent des zone principalement résidentielles. C’est, par exemple, comme ça que s’est organisée Houston et nous avons vu que ça n’est ni un effet du hasard ni une volonté du planificateur ; il se trouve que le centre est, par construction, le point de la ville qui minimise la distance moyenne (et donc, modulo quelques hypothèses, le temps de trajet) nécessaire pour s’y rendre.

Alain Bertaud, dans Order without Design, propose un modèle très simple qui permet d’estimer la densité résidentielle, en nombre d’habitants par unité de surface au sol, en fonction de la distance au centre. Avec d₀, la densité du centre et g, le gradient de densité, la densité d_x atteinte à x km du centre est donnée par¹ :

\(d_x = d_0 \times e^{-gx}\)

Ce qui, illustré en 3D, donne une forme comme celle que j’ai utilisé en en-tête de cet article : la densité baisse quand on s’éloigne du centre et elle tend à baisser plus rapidement lorsqu’on est proche du centre que lorsqu’on en est loin.

Alain Bertaud a testé cette formule sur un certain nombre de villes partout dans le monde et il semble qu’elle décrit assez fidèlement ce qu’on observe sur le terrain (il trouve des R² qui tournent autour de 0.9²) sauf dans deux types d’agglomérations : celles qui ont des topographies très contraignantes (Rio de Janeiro et ses parcs naturels en pleine ville) et celles qui résultent d’un exercice de pure planification (Moscou au début des années 1990). Partout ailleurs, on arrive généralement à fitter les densités réelles avec ce modèle — c’est même le cas, pour des raisons sur lesquelles je reviendrai une autre fois, dans les villes dépourvues de centre.

Le paramètre important, évidemment, c’est le gradient de densité (g) qui détermine à quelle vitesse la densité décroît au fur et à mesure qu’on s’éloigne du centre. Plus g est élevé plus la pente de la courbe est importante et inversement. La prédiction centrale de la théorie, si on admet que le coût d’un trajet est directement proportionnel à la distance parcourue, c’est que plus les transports sont coûteux — financièrement mais aussi en termes de valeur du temps — plus le gradient est élevé ; c’est-à-dire que la densité décroît plus rapidement quand on l’éloigne du centre.

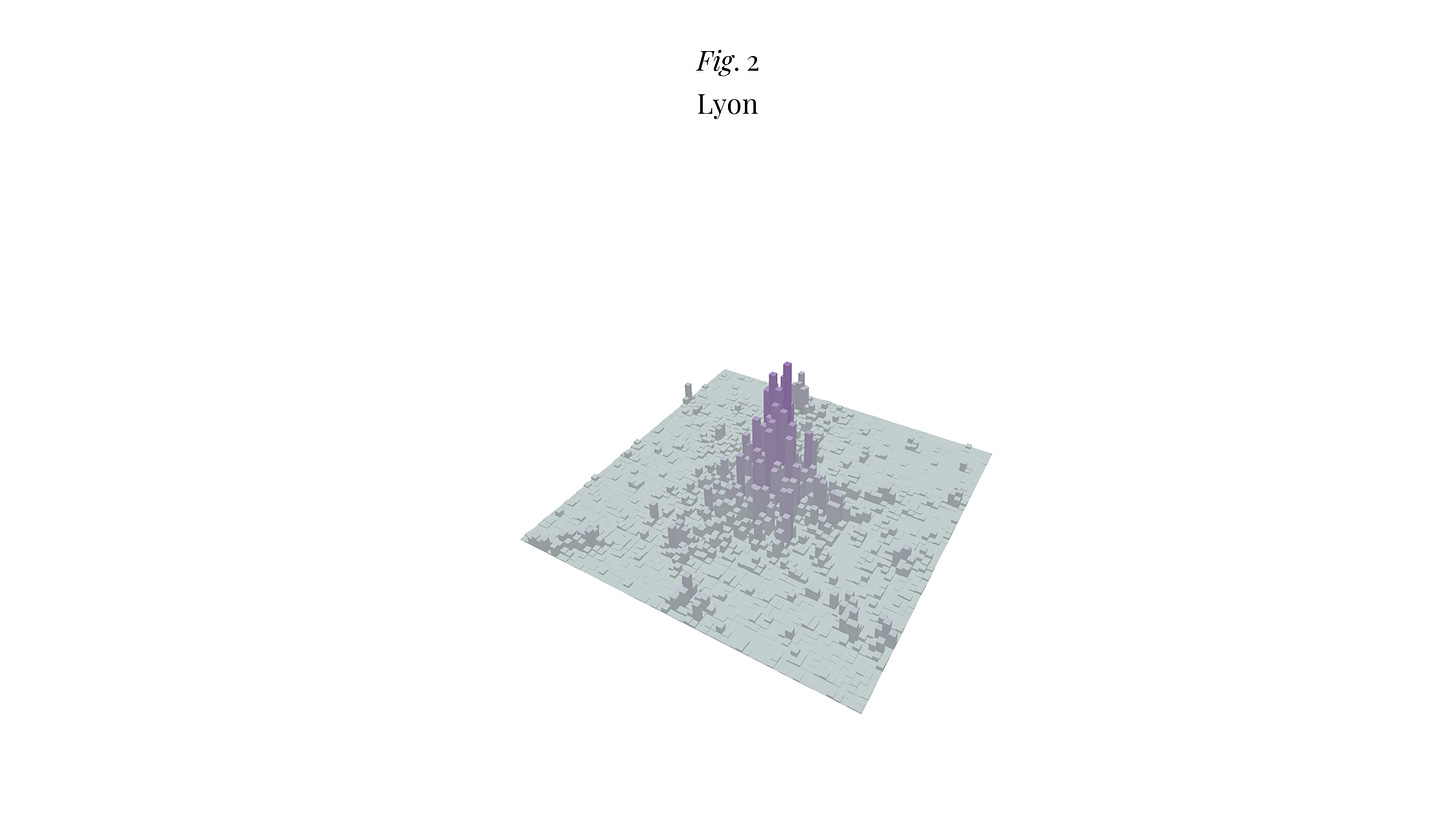
Pour illustrer cette idée, j’ai utilisé les données de l’Insee avec des carreaux d’un kilomètre de côté³ pour construire des cartes de densité de 60 km de côté, centrées sur les mairies de Paris, Lyon et Marseille⁴, et tester le modèle sur ces trois zones urbaines (vous trouverez le code utilisé en fin d’article). Autant le dire tout de suite : mes R² ne sont pas aussi élevés que ceux que trouve Bertaud mais ça peut être dû à un problème de méthode (i.e. j’utilise absolument tous les carreaux pour lesquels j’ai une densité non-nulle, y-compris des espaces naturels non-constructibles).

Pour Paris, je trouve un gradient de 0.13 (ce qui est très proche des 0.1 mesurés par Bertaud) avec un R² 0.62. Le pic de densité est à 46’551 habitants/km².

Pour Lyon, j’ai un gradient de 0.27 et un R² de 0.53. Notez que ce graphe est à la même échelle que celui de Paris : le pic de densité est à 23’296 habitants/km².

Pour Marseille, enfin, je trouve un gradient de 0.25 et un R² de 0.56. Le pic de densité est quasiment identique à celui de Lyon avec 23’358 habitants/km².

Bref, les gradients de Lyon et Marseille sont deux fois plus élevés que celui de Paris ce qui, vous en conviendrez, n’est absolument pas surprenant⁵. Quant au modèle lui-même, il « capte » manifestement quelque chose même si, encore une fois, on n’est pas au niveau des R² trouvés par Bertaud ; ce qui amène naturellement à se demander comment on pourrait l’améliorer. Je vois principalement deux pistes.

La première, c’est de ne pas chercher à estimer la densité résidentielle mais quelque chose de plus générique comme la surface de plancher, le coefficient d’occupation des sols⁶ ou, peut-être mieux encore, le prix au m² de plancher. La raison en est fort simple : le centre tend à attirer de la surface de bureaux et des commerces lesquels, par effet d’éviction, contribuent à repousser l’espace résidentiel autour d’eux. L’exemple typique, c’est le 8e parisien, au cœur du quartier central des affaires : c’est le 3e arrondissement le moins peuplé de Paris (9'136 habitants/km²) mais c’est aussi le 3e arrondissement le plus dense en termes d’emplois (47'306 emplois au km²).

La seconde consiste à ne pas expliquer ce qui précède par des distances — et surtout pas des distances à vol d’oiseau — mais par des coûts de trajet ; ce qui inclue une dimension sonnante et trébuchante (le coût de votre pass Navigo, par exemple) mais aussi la valeur du temps. En première approximation, on peut considérer qu’un trajet de 10 km en voiture coûte à peu près la même chose dans tous les centres-villes de France mais ça prend un peu plus de 26 minutes à Paris contre environ 16 minutes à Lyon ou à Marseille.

Évidemment, tout ça implique un certain nombre de données dont je ne dispose malheureusement pas. Nous en resterons donc là pour le moment. Reste que ce modèle, même dans sa forme rudimentaire, introduit de façon tout à fait crédible une relation générale entre pouvoir d’attraction du centre, mobilité et densité de la périphérie.

---

Voici le code R que j’ai utilisé. Il est loin d’être optimisé : j’ai cherché à le rendre aussi lisible que possible. Notez que vous pouvez afficher autre chose que des densités.

# Préalable :
# install.packages("plot3D")

library(plot3D)

# Avec votre chemin d'accès :
X <- read.csv(".../carreaux_1km_met.csv")

ins <- X$idcar_1km
e <- as.numeric(substr(ins, 25, 31))
n <- as.numeric(substr(ins, 17, 23))

# Nombre d'habitants par carreau :
ind <- X$ind

# Toute la France métropolitaine :
Z <- tapply(ind, list(e, n), mean)
x <- as.numeric(colnames(Z))
y <- as.numeric(rownames(Z))

# Paramètres graphiques :
ray <- (-30:30)
brk <- seq(0, 50000, 1000)
col <- colorRampPalette(c("azure2", "darkorchid"))
phi <- 30
theta <- 30

# Matrice de distances :
Dmat <- matrix(NA, 61, 61)
for(i in 1:nrow(Dmat)) {
	for(j in 1:ncol(Dmat)) {
		h <- abs(i-31)
		v <- abs(j-31)
		Dmat[i, j] <- sqrt(h^2+v^2)
	}
}

# -------------------------------------------------------------
# Paris (Mairie : CRS3035RES1000mN2889000E3760000)
xi <- 2889000
yi <- 3760000
Paris <- Z[which(y == yi)+ray, which(x == xi)+ray]
Paris[is.na(Paris)] <- 0

hist3D(z = Paris, phi = phi, theta = theta, zlim = c(0, 50000), axes = F,
	border = NA, colkey = F, col = col(length(brk)-1), breaks = brk,
	box = FALSE, shade = .2)

dens <- as.numeric(Paris)
dist <- as.numeric(Dmat)
ii <- !is.na(dens) & dens > 0 & dist > 0
dens <- dens[ii]
dist <- dist[ii]
model <- nls(dens~a*exp(-b*dist),
	start = list(a = dens[floor(length(dens)/2)], b = -.1))
co <- coef(model)
xx <- 0:40
plot(dist, dens)
lines(xx, co[1]*exp(-co[2]*xx), col = "red")
grad <- round(co[2], 2)
r2 <- round(1-(deviance(model)/sum((dens-mean(dens))^2)), 2)

# -------------------------------------------------------------
# Lyon (Mairie : CRS3035RES1000mN2531000E3919000)
xi <- 2531000
yi <- 3919000
Lyon <- Z[which(y == yi)+ray, which(x == xi)+ray]
Lyon[is.na(Lyon)] <- 0

hist3D(z = Lyon, phi = phi, theta = theta, zlim = c(0, 50000), axes = F,
	border = NA, colkey = F, col = col(length(brk)-1), breaks = brk,
	box = FALSE, shade = .2)

dens <- as.numeric(Lyon)
dist <- as.numeric(Dmat)
ii <- !is.na(dens) & dens > 0 & dist > 0
dens <- dens[ii]
dist <- dist[ii]
model <- nls(dens~a*exp(-b*dist),
	start = list(a = dens[floor(length(dens)/2)], b = -.1))
co <- coef(model)
xx <- 0:40
plot(dist, dens)
lines(xx, co[1]*exp(-co[2]*xx), col = "red")
grad <- round(co[2], 2)
r2 <- round(1-(deviance(model)/sum((dens-mean(dens))^2)), 2)

# -------------------------------------------------------------
# Marseille (Mairie : CRS3035RES1000mN2254000E3944000)
xi <- 2254000
yi <- 3944000
Marseille <- Z[which(y == yi)+ray, which(x == xi)+ray]
Marseille[is.na(Marseille)] <- 0

hist3D(z = Marseille, phi = phi, theta = theta, zlim = c(0, 50000), axes = F,
	border = NA, colkey = F, col = col(length(brk)-1), breaks = brk,
	box = FALSE, shade = .2)

dens <- as.numeric(Marseille)
dist <- as.numeric(Dmat)
ii <- !is.na(dens) & dens > 0 & dist > 0
dens <- dens[ii]
dist <- dist[ii]
model <- nls(dens~a*exp(-b*dist),
	start = list(a = dens[floor(length(dens)/2)], b = -.1))
co <- coef(model)
xx <- 0:40
plot(dist, dens)
lines(xx, co[1]*exp(-co[2]*xx), col = "red")
grad <- round(co[2], 2)
r2 <- round(1-(deviance(model)/sum((dens-mean(dens))^2)), 2)

1. Les financiers parmi nous aurons peut-être reconnu la formule d’actualisation d’un cash-flow futur avec des taux composés en continu. Conceptuellement, c’est la même idée : remplacez d₀ par la valeur future du cash-flow, d_x par sa valeur actuelle, x par le temps (en années) qui sépare les deux et g est un taux d’intérêt composé en continu — lequel (spoiler) reflète la valeur-temps de l’argent (éventuellement augmentée d’une prime de risque).

2. Ce qui, pour un modèle aussi simple et alors que nous savons que la réalité est infiniment plus complexe, est assez remarquable.

3. Ce sont des données de 2019 que vous retrouverez sur les cartes de Géoportail (Économie et statistiques / Démographie / Densité de population). Elles existent aussi avec des carreaux d’un km de côté mais à cette échelle très fine, on a plus de bruit qu’autre chose.

4. Mes cartes mesurent 60 km de côté de telle sorte que le carré central (de 1x1 km) soit celui dans lequel se trouve la mairie. Vous trouverez les identifiants des carreaux centraux dans le code ci-dessus.

5. Pour mémoire : à Lyon, le métro et le tramway offrent 12 lignes pour 118.2 km de réseau et à Marseille, c’est à peine 5 lignes pour 35.7 km de réseau.

6. La surface de plancher par mètre carré de terrain.