L'effet Broadway
Les plans de rue orthogonaux tendent à rallonger les distances mais une simple modification peut les rendre très efficients.
En général, on considère qu’un adulte normal marche à 1.3 m/s (4.68 km/h) mais l’expérience démontre que les gens marchent en général plus vite dans les grandes villes et ce, d’autant plus qu’elles sont productives. Pour la suite, je vais utiliser 1.414 m/s (soit 5.09 km/h) parce que c’est une valeur tout à fait raisonnable et parce que ça m’arrange.
Par ailleurs, on considère habituellement que la zone d’attraction d’une station de transport en commun (en site propre) c’est environ 10 minutes de marche — c’est le temps que vous acceptez de marcher pour rejoindre la station, et c’est d’autant plus vrai que le système de TC est rapide. Ça nous donne donc un maximum de 848.5 mètres de marche.
Enfin, nous avons vu la dernière fois qu’un des principaux facteurs qui limite la vitesse de nos transports en commun, c’est la taille des interstations : plus elles sont éloignées les unes des autres, plus il est possible de rouler vite et moins vous perdez de temps en arrêts intermédiaires. Sauf qu’évidemment, des stations très espacées, ça implique aussi plus de marche.
De là, je me suis livré à un petit exercice de style qui consiste à essayer d’évaluer l’écartement maximal entre deux stations de telle sorte que personne ne vive (ou ne travaille) à plus de 10 minutes de marche de la station la plus proche. Ça dépend évidemment du plan des rues et la pire des situations (hors cas très spécifiques), c’est la distance de Manhattan.
Supposez, pour simplifier, que nous ayons une grille régulière de 36 blocs (i.e. îlots) carrés de 100 mètres de côté, séparés par des rues perpendiculaires (on va supposer que l’emprise des rues est rognée sur les blocs). La station est en bas, à droite (c’est le point rouge plein) et nous allons voir ce qu’il se passe quand vous partez d’une des autres 48 intersections.
La Fig. 1 décrit le cas idéal : la ligne droite. En l’occurrence, vous avec 6 blocs à passer et donc 600 mètres à parcourir, ce qui ne vous pendra que 7 minutes et 4 secondes. Les urbanistes utilisent la notion de facteur de détour : la distance effectivement parcourue rapportée à la distance à vol d’oiseau ; ici ça donne 600/600 et donc un facteur de détour de 1.
En revanche, ça se corse avec la Fig. 2 : le schéma des rues vous oblige à zigzaguer en angles droits. En l’occurrence, vous allez devoir parcourir 900 mètres pour un distance à vol d’oiseau d’environ 670.8 mètres (le théorème de Pythagore est votre ami) ce qui nous donne un facteur de détour de l’ordre de 1.342.
La Fig. 3, pour finir, c’est le pire des cas : c’est toute la diagonale que vous devez parcourir en zigzagant. Ça nous donne 1'200 mètres de marche (et donc, on est hors budget) pour une distance à vol d’oiseau d’à peu près 848.5 mètres ; soit un facteur de détour d’environ 1.414 (i.e. la racine carrée de 2).
Celles et ceux d’entre vous qui ont eu l’occasion de comparer l’ont sans doute remarqué : pour une distance à vol d’oiseau identique, on marche significativement plus à Manhattan qu’à Paris et c’est d’autant plus vrai qu’on circule dans un quartier très quadrillés (Upper East Side, par exemple) et sur de courtes distances (quand vous contournez un bloc, le facteur de détour approche 2).
Dans mon exemple et en supposant que toutes les intersections sont des points de départs équiprobables (sauf celle de la station, bien sûr), on peut calculer que les habitants marchent en moyenne 612.5 mètres avec un facteur de détour de 1.25 (on a 12 trajets en ligne droite et 36 en zigzags) — autrement dit, le plan des rues allonge les distances de 25% en moyenne.
Ceci étant dit, il ne faut pas dénigrer le plan orthogonal des rues de Manhattan trop vite parce qu’il y a aussi des diagonales — la plus célèbre étant sans doute Broadway — et vous allez voir que ça peut radicalement changer la donne. Ci-dessous, j’ai simplement rajouté une grande rue piétonne sur la diagonale qui amène à ma station ; vous pouvez aussi y rajouter des pistes cyclables auquel cas 20 mètres de large et donc une emprise de l’ordre de 17'000 m² est plus que confortable et ne représente que 4.7% de la surface totale de mon schéma.
Le résultat (Fig. 4), c’est que mon intersection la plus éloignée est désormais à 848.5 mètres, et donc 10 minutes à pied, de la station (facteur de détour de 1) — mission accomplie ! — mais si vous y regardez de plus près, vous observerez que ma diagonale raccourcit aussi les distances des 35 autres trajets qui étaient précédemment en zigzag (Fig. 5 et Fig. 6). En moyenne, avec la même hypothèse d’équiprobabilité des points de départs, la distance moyenne parcourue passe à 501.4 mètres (soit une baisse de 18.1%) et on obtient un facteur de détour moyen d’à peine 1.041 — ce qui est extrêmement faible, c’est-à-dire très proche de la ligne droite.
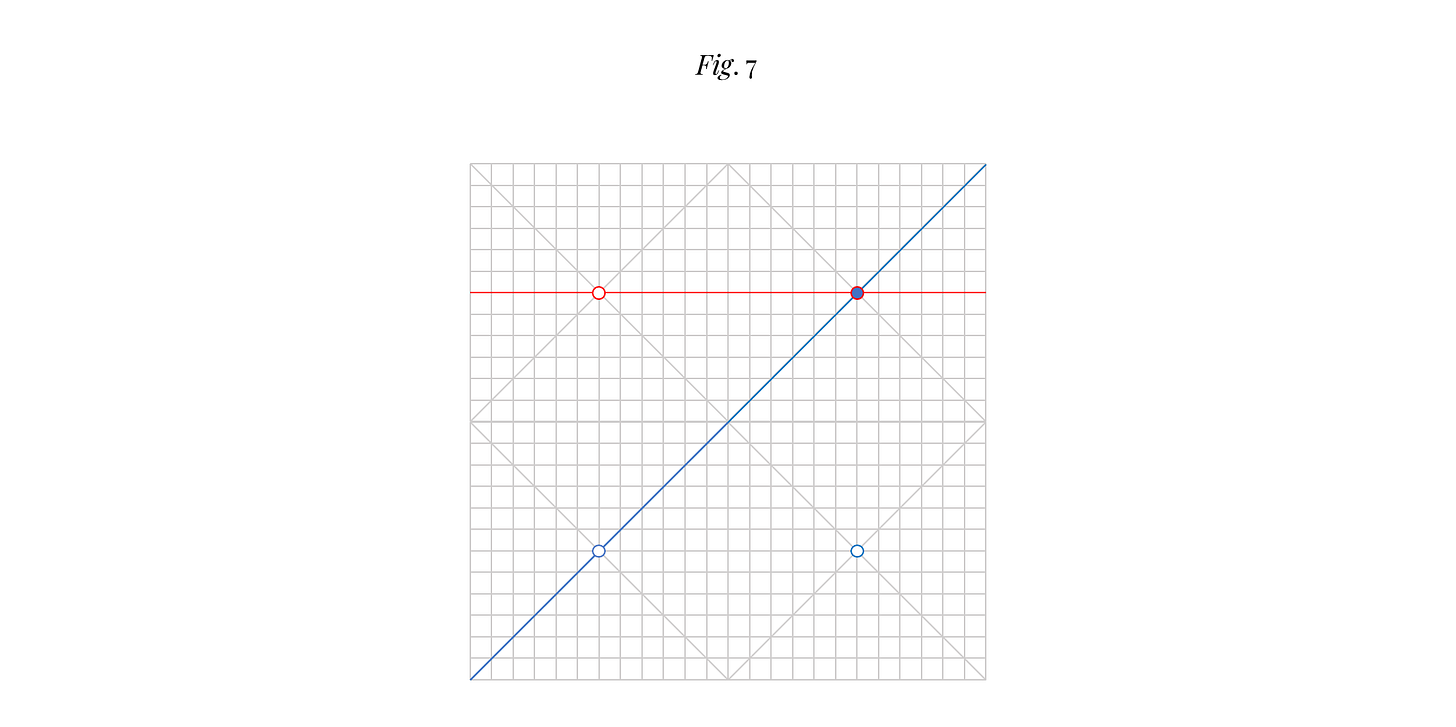
Évidemment, notre station a vocation à être centrale. C’est-à-dire qu’elle est pensée pour desservir quatre zones comme celle décrite ci-dessus ; lesquelles, collées les unes aux autres, peuvent donner quelque chose comme ça :
Ce qui nous donne, au choix ou cumulativement, des interstations de 1'200 mètres (ligne rouge) ou d’environ 1'700 mètres (ligne bleue).
Pour information, avec des hypothèses très raisonnables (9 stations, 90 km/h en vitesse de croisière, des accélérations de 1 m/s² et des arrêts à quai de 30 secondes), la ligne rouge vous permet de parcourir 12 km en un peu moins de 15 minutes — rajoutez 10 minutes de marche au départ et autant à l’arrivée et vous avez une ville de la taille de Paris (hors bois) dans laquelle le trajet le plus long qu’il soit possible de faire tient en 35 minutes, mettons 40 pour tenir compte des temps d’attente et des éventuelles ruptures de charge (sachant que la combinaison marche + TC est systématiquement plus rapide que la voiture, sur tous les trajets possibles et d’assez loin).
Il va de soi que tout ça est très schématique mais cette histoire de diagonale méritait, il me semble, qu’on la note dans un coin.
Calcul socioéconomique (de coin de table) : grâce à cette diagonale, un habitant moyen gagne 1 minute et 19 secondes sur son temps de trajet et donc, avec des allers-retours quotidiens (travail, études), 2 minutes et 37 secondes par jour. En retenant 218 jours travaillés par an et une valeur du temps de 12 euros de l’heure (rapport Quinet actualisé), ça nous fait un peu plus de 114 euros par an et par personne. Si elle ne profite qu’à 3'000 travailleurs et étudiants (ce qui semble peu pour une zone urbaine de 360'000 m²), ça fait 342'382 euros par an qui, actualisés sur 10 ans (à peine) au taux des emprunts d’État français (le 10 ans est à 2.544% à l’heure où j’écris ces lignes), nous donne une valeur d’un peu plus de 3.5 millions d’euros par kilomètre.
Crédit photo : The New York Times.